|

The theory of gas chromatography, presented by the equation of Van Deemter,
 (1) (1)
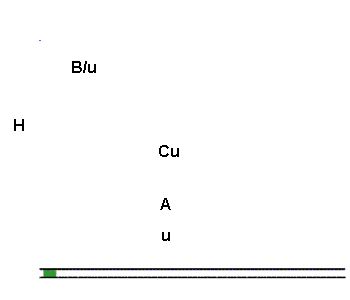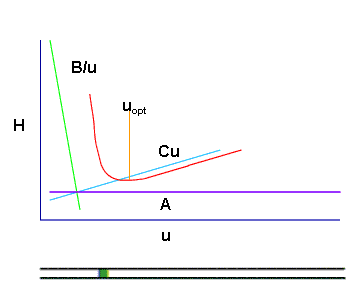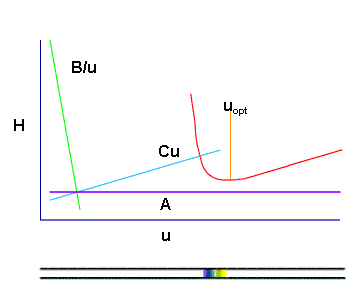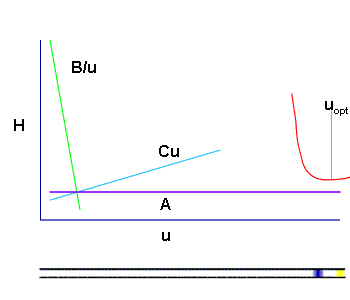
shows that for each chromatographic separation there exists an optimal flow rate above and below which the column efficiency is reduced.
In practice, the linear speed of the sample zone moved by the carrier gas, is changed continuously and increases as it approaches the outlet, which results in a non-effective use of a part of the column.
In this case equation (1) characterizes the optimal separation process only in that section of the chromatographic column through which the sample passes at an optional speed.
In equation (1)  are constant values and are constant values and  is the speed of the moving zone of the sample which changes continuously in time. Thus equation (1) gets the following form: is the speed of the moving zone of the sample which changes continuously in time. Thus equation (1) gets the following form:
 (2) (2)
where  is the speed of the sample at a distance is the speed of the sample at a distance  from the beginning of the column and changes - increases - toward the outlet. This shows that HETP is not always optimal in all sections of the chromatographic column. from the beginning of the column and changes - increases - toward the outlet. This shows that HETP is not always optimal in all sections of the chromatographic column.



Let  be the length of the chromatographic column, be the length of the chromatographic column,  the pressure at the inlet of the column and the pressure at the inlet of the column and  the pressure at the outlet of the column, the pressure at the outlet of the column,  the distance of a point on the chromatographic column from its inlet. the distance of a point on the chromatographic column from its inlet.
It is evident that pressure  at point at point  on the column can be determined from the correlation on the column can be determined from the correlation

The flow rate  at any point on the at any point on the  chromatographic column depends on pressure chromatographic column depends on pressure  at that point, as well as on the inlet pressure at that point, as well as on the inlet pressure  and the outlet pressure and the outlet pressure  of the column. But the pressure of the column. But the pressure  at any point on the column depends on the inlet pressure at any point on the column depends on the inlet pressure  and the outlet pressure and the outlet pressure  of the chromatographic column and on the distance of the chromatographic column and on the distance  from the column inlet. Thus the flow rate from the column inlet. Thus the flow rate  at any point at any point  on the column in case of fixed physical parameters of the chromatographic column can be considered as a function of pressure at this point and at the ends and of the distance of this point from the column inlet; on the column in case of fixed physical parameters of the chromatographic column can be considered as a function of pressure at this point and at the ends and of the distance of this point from the column inlet;

Consequently the whole process in the chromatographic column is characterized by a multiple of equations (3).

When at the inlet and outlet of the column the pressure is kept constant, each section of the chromatographic column, through which the sample zone moves, is characterized by its equation from multiple (3).
However the linear speed of the sample zone moving with the carrier-gas can be kept constant by programming the pressure gradient movement along the column in time, realizing the function: pressure - location - time by keeping constant the pressure difference ∆ p at the ends of the chromatographic column during the whole cycle of the analysis (Russia Patent "Chromatograph of A. S. Hayrapetyan").
The sample travels through the chromatographic column in time

where  is the length of the chromatographic column and is the length of the chromatographic column and  the optimal speed of the sample zone. the optimal speed of the sample zone.
The pressure at the inlet and outlet of the chromatographic column, undergoing a change at equal intervals of time, is expressed by

where  - sample injection time, and - sample injection time, and  - elution time. - elution time.
We mark by

the sections of the chromatographic column travelled by the sample zone with an optimal velocity of the carrier-gas at the corresponding moments of time,

where  - the beginning of the chromatographic column, and - the beginning of the chromatographic column, and 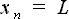 - the end of the chromatographic column. - the end of the chromatographic column.
Let at the moment  the pressure at the inlet and outlet of the chromatographic column be correspondingly the pressure at the inlet and outlet of the chromatographic column be correspondingly

Then at the moments of time  on the corresponding sections on the corresponding sections

of the chromatographic column, the pressure will be

It may be noticed that

as well as

in this case
 à à 
We build a matrix of pressures in the following way: let each line in it correspond to the pressures of the column at points

at a pressure  at the inlet and at the inlet and  at the outlet of the column at a moment at the outlet of the column at a moment  while each column corresponds to the pressures at a point while each column corresponds to the pressures at a point  at moments of time at moments of time

Thus the matrix has the following form

The first column of the matrix corresponds to the pressure at the inlet of the column, while the last one to the outlet. They are chosen such that in the column zone where the sample is found at a definite moment of time, there will always exist a constant pressure corresponding to an optimal flow rate. The first column corresponds to the moment of sample introduction, and the last one to the elution of the separated components from the column. Each element of the matrix corresponds to a definite flow rate at a definite moment of time. To each element of the matrix there corresponds a definite flow rate and followingly its equation from the multiple (3). The matrix elements corresponding to the passage of the sample with an optimal speed through the corresponding points of the column at definite moments of time are marked in yellow. For these it may be written

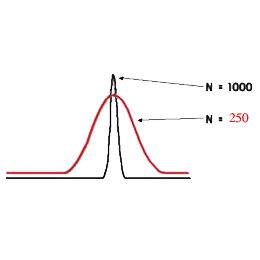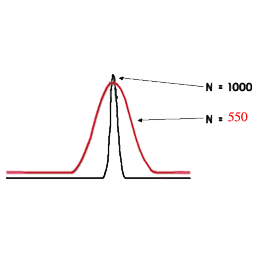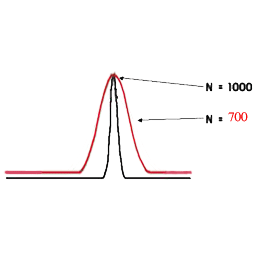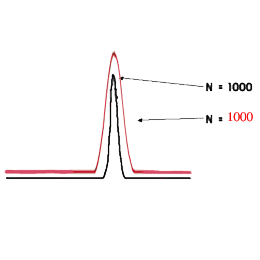
The carrier-gas pressure is programmed in such a way that it constantly secures an optimal linear speed for an imaginary point - the zone of the sample which travels with the carrier-gas from the inlet to the outlet of the chromatographic column in time, keeping ∆ p constant at its ends during the whole cycle of the analysis. This arithmetical model (of Hayrapetyan - Aghababyan) of chromatographic analysis built on the basis of the equation of Van Deemter describes in detail the mentioned technological process of analysis organization and corresponds to that equation from the multiple (3) which provides the optimal conditions of the analysis and leads to the attainment of the maximum possible efficiency of the column (Hayrapetyan's Effect).
In other words the pressure at the inlet and outlet of the chromatographic column is programmed such, that the carrier-gas flow rate in the column is optimal in each section at the needed moments of time. Thus, the separation of the sample is characterized by the equations from the multiple (3)

and they are all equivalent to the equation
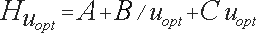 (4) (4)
And thus the maximum possible efficiency of the chromatographic column is attained (Hayrapetyan's Effect).

|